PDFO documentation#

Version:: 2.1
Downloads:: 305,692
Author of solvers:: M. J. D. Powell
Authors of PDFO:: Tom M. Ragonneau | Zaikun Zhang

PDFO is a cross-platform package providing the late Professor M. J. D. Powell’s derivative-free (i.e., zeroth-order) optimization solvers. Using only function values, but not derivatives, it solves problems of the form

\[\begin{split}\min_{x \in \R^n} \quad \obj ( x ) \quad \text{s.t.} \quad \begin{cases} \xl \le x \le \xu,\\ \aub x \le \bub, ~ \aeq x = \beq,\\ \cub ( x ) \le 0, ~ \ceq ( x ) = 0. \end{cases}\end{split}\]

To install PDFO for Python, run in your terminal

pip install pdfo

You can also check the installation guide for MATLAB. For more details, see the user guide.

Citing PDFO#

If you would like to acknowledge the significance of PDFO in your research, we suggest citing the project as follows:

T. M. Ragonneau and Z. Zhang. “PDFO: a cross-platform package for Powell’s derivative-free optimization solvers.” 2023. DOI: 10.48550/arXiv.2302.13246. arXiv: 2302.13246 [math.OC].

The corresponding BibTeX entry is given hereunder.

@unpublished{pdfo,
    author       = {Ragonneau, T. M. and Zhang, Z.},
    title        = {{PDFO}: a cross-platform package for {P}owell's derivative-free optimization solvers},
    eprint       = {2302.13246},
    eprinttype   = {arxiv},
    eprintclass  = {math.OC},
    year         = 2023,
    doi          = {10.48550/arXiv.2302.13246},
}

Statistics#

As of December 21, 2024, PDFO has been downloaded 305,692 times, including

1,334 times on GitHub,
215,824 times on PyPI (mirror downloads excluded), and
88,534 times on Anaconda.

The following figure shows the cumulative downloads of PDFO.

(Source code, png, hires.png, pdf)

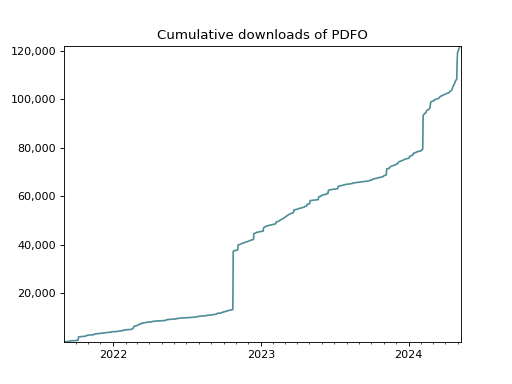
We started tracking the downloads of PDFO on Anaconda on October 2022. The API we employ to track the downloads of PDFO on Anaconda only provides the cumulative downloads. Therefore, we do not know when the downloads of PDFO on Anaconda have been made. In this plot, all of them are assumed to have been made on October 2022.

Acknowledgments#

PDFO is dedicated to the memory of the late Professor M. J. D. Powell with gratitude for his inspiration and for the treasures he left to us. We are grateful to Professor Ya-xiang Yuan for his everlasting encouragement and support.

The development of PDFO is a long-term project, which would not be sustainable without the continued funds from the Hong Kong Research Grants Council (ref. PolyU 253012/17P, PolyU 153054/20P, and PolyU 153066/21P), the Hong Kong PhD Fellowship Scheme (ref. PF18-24698), and The Hong Kong Polytechnic University (PolyU), in particular the Department of Applied Mathematics (AMA).